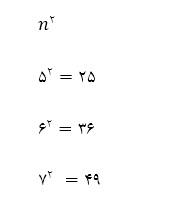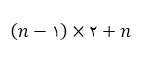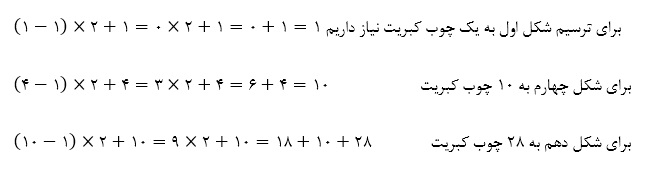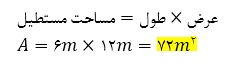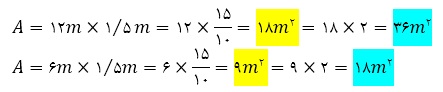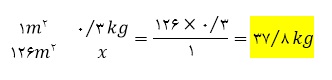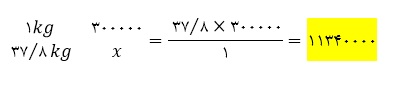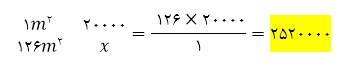پلی لیست ریاضی هفتم فصل 1 (راهبردهای حل مسئله)
جزوه ریاضی هفتم فصل 1 راهبردهای حل مسئله (8 صفحه)دانلود
فیلم و جزوه طول سال ریاضی هفتم فصل اول راهبردهای حل مسئله – قسمت اول
چگونه مسئله را حل کنیم؟
حل کردن هر مسئله 4 مرحله دارد. هر وقت قرار است مسئله ای را حل کنید(مسئله هر کتاب) این 4 مرحله را به ترتیب در نظر داشته باشید تا به نتیجه مطلوب برسید.
مرحله اول در حل مسئله ریاضی : فهمیدن مسئله
در مرحله اول مسئله را با دقت کامل بخوانید. قبل از اینکه به دنبال راه حل بگردید و سعی بر حل کردن مسئله نماید ، باید کمی سرعت خود را کم کنید و کل مسئله را یک بار (و حتی دو بار) بخوانید. این به شما کمک میکند تا تصویر بزرگتر و کاملتری داشته باشید و خواسته مسئله را دریابید.
بعضی اوقات, بدون دلیل، اطلاعات اضافه در مسئله گنجانده میشود. شما باید بتوانید تمرکز خود را حفظ کنید، آن جزئیات اضافی را نادیده بگیرید و دریابید که سؤال واقعی در آن مسئله چه چیزی است. و مسئله از شما چی خواسته است.
مرحله دوم در حل مسئله ریاضی: انتخاب راهبرد مناسب
در این مرحله باید یک راهبرد مناسب به مسئله مورد نظر دریافت کنید. راهبرد های حل مسئله مراحلی هستند که شخص برای یافتن مشکلاتی که در مسیر رسیدن به هدف خود قرار دارند، از آنها استفاده می کند. این راهبرد ها میتواند شامل: رسم و شکل, الگو سازی, حدس و آزمایش و… باشد.
مرحله سوم در حل مسئله ریاضی: حل کردن مسئله
با راهبردی که انتخاب کرده اید مسئله را حل کنید. اگر تشخیص داده اید که این راهبرد برای حل مسئله شما نتیجه نمیدهد برگردید به مرحله قبلی و راهبرد جدید انتخاب کنید
مرحله چهارم در حل مسئله ریاضی: بازگشت به عقب
حل مسئله فقط با دریافتن جواب ریاضی تمام نمیشود. باید برگردیم به عقب و ببینیم که مسئله از ما چی خواسته است؟ آیا ما به جواب نهایی مسئله رسیدیم؟ شاید مسئله یک موضوع تحلیلی داشته باشد پس بعد از اینکه جواب ریاضی آنرا دریافت کردیم, بر میگردیم به عقب و به کمک جواب دریافتی ریاضی ما بخش تحلیلی مسئله را نیز حل میکنیم تا مسئله ما به طور کامل حل گردد.
ریاضی هفتم فصل اول شامل درس های: 1- راهبرد رسم و شکل 2- راهبرد الگوسازی 3- راهبرد حذف حالت های نامطلوب 4- راهبرد الگویابی 5- راهبرد حدس و آزمایش 6- راهبرد زیر مساله 7-راهبرد حل مساله ساده تر و 8- راهبرد روش ها نمادین میباشد.
در مراحل حل مسئله, مرحله دوم آن انتخاب راهبرد مناسب است. در اینجا ما چندین راهبرد برای حل مسائل را مورد مطالعه قرار میدهیم.
راهبرد رسم و شکل
راهبرد رسم شکل راهبرد شهودی است. بعضی از مسئله ها را میتوان با استفاده از این راهبرد به راحتی حل کرد. و برای بعضی مسئله های دیگر نیز میتوان به کمک این راهبرد رسم و شکل راهبرد مناسب و دقیق برای حل آنها دریافت.
در ریاضی هفتم صفحه 2 راهبرد رسم و شکل آمده است . راهبرد رسم و شکل مهمترین راهبرد در حل یک مسئله میباشد که ما اکثراً در حل مسائل از این راهبرد مهم استفاده میکنیم. و 3 مسئله که در این صفحه است , در این فیلم آموزشی به وضاحت تمام حل گردیده است.
راهبرد الگوسازی
الگوسازی چیست؟
الگو سازی در ریاضی به معنای کشف رابطه و نظم موجود بین مسئله ها میباشد.
گاهی وقتها در بعضی از مسئله ها تمام حالت های ممکن خواسته میشود. در این گونه مواقع بهتر است برای حل مسئله از راهبردهای الگوسازی استفاده کنیم و با رسم یک جدول منظم، اعداد و ارقام و داده های مسئله را مرتب کرده تا بتوانیم تمام حالت های صحیح برای جواب مسئله را به دست آوریم.
کتاب ریاضی هفتم صفحه 3 در مورد راهبرد الگو سازی میباشد که الگو مبحث خیلی مهم و کاربردی در بخش ریاضیات است و در پایه های بالا هم کاربرد اساسی دارد.
اعداد طبیعی
اعدادی هستند که از یک شروع میشود و تا بینهایت (عدد n ) ادامه دارند. و شامل صفر نمیشود.
به بیان ساده، عدد طبیعی، عددی است که در طبیعت وجود دارد و برای شمردن عناصر طبیعی استفاده میشوند، برای مثال عدد صفر یا اعداد منفی در طبیعت وجود ندارند و در مجموعه اعداد طبیعی نیستند.
مثال: دو عدد طبیعی را پیدا کنید که حاصل ضرب آنها 24 و حاصل جمع آنها کمترین مقدار ممکن باشد. جدول را با نظم و ترتیب کامل کنید.
حاصل جمع | دومین عدد | اولین عدد |
25 14 11 10 | 24 12 8 6 | 1 2 3 4 |
ریاضی هفتم صفحه 4 شامل راهبرد مهم دیگری در حل مسائل میباشد, که این راهبرد , راهبرد حذف حالت های نامطلوب است.
راهبرد حذف حالت های نامطلوب:
به شرایط و اطلاعات مسئله توجه کنید و حالت های نامطلوب و نادرست را کنار بگذارید؛ آن گاه پاسخ مسئله یا
همان حالت های مطلوب به دست می آیند. و بعدا میتوانیم با استفاده از الگو سازی جدول و شکل منظم برای مسئله درست کرده و مسئله را حل کنیم.
اعداد حسابی:
اعداد حسابی همان اعداد طبیعی در دستگاه اعداد عربی هستند که صفر هم به آنها اضافه شدهاست. به اعداد حسابی اعداد صحیح نامنفی هم گفته میشود.
راهبرد الگویابی:
یکی از مباحث بسیار مهم در ریاضی مبحث الگوهای عددی و هندسی است. دو نوع الگو برای دانش آموزان معرفی می شود که عبارتند از:
- الگوهای عددی
- الگوهای هندسی
تفاوت الگوهای عددی و هندسی در چیست؟
الگوهای عددی همانطور که از اسم آن مشخص است با اعداد مشخص می شوند و هر یک از اعداد در الگو، جملات الگو نامیده می شوند. مثلا جمله سوم الگوی عددی زیر برابر با 5 است.
1,3,5,7……
الگوهای هندسی با رسم شکل مشخص می شوند و در آنها با شماره شکل الگو سر و کار داریم.
در الگوهای عددی، باید یک رابطه ای بین جملات الگو ( اعداد داده شده در الگو ) را پیدا کرد و سپس با استفاده از رابطه به دست آمده جملات دیگر الگو را محاسبه نمود اما در الگوهای هندسی باید بتوانیم تشخیص دهیم که شکلهای الگو بر چه اساسی رسم شده اند و شکلهای بعدی را نیز رسم کنیم و تعداد اشیایی که در ساخت شکلها به کار می روند را حساب کنیم.
حل مسائل ریاضی هفتم صفحه 4 و 5 را میتوانید در این فیلم آموزشی مشاهده کنید.
حل مسائل ریاضی هفتم صفحه 5 :
مثال الگوی عددی: سه عدد بعدی الگوی زیر را بنویسید.
1,4,9,16,…….
الگوی بالا بر اساس مربع اعداد طبیعی ترتیب شده است.
پس سه عدد بعدی الگوی بالا 36,25و 49 میباشد.
1,4,9,16,25,36,49…
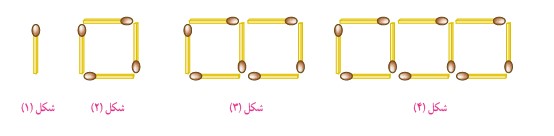
مثال الگوی هندسی: شکل دهم با چند چوب کبریت ساخته میشود ؟چرا؟
الگو برای شکل بالا قرار ذیل میباشد:
در اینجا n شماره شکل ما را شامل میشود, یعنی اگر بخواهیم تعداد چوب کبریت شکل اول را بدست بیاریم بجای n عدد 1 را میگذاریم. و یا اگر بخواهیم تعداد چوب کبریت برای شکل های 4 و دهم را دریابیم بجای n اعداد مورد نظر را میگذاریم.
راهبرد حدس و آزمایش
ممکن است یک مسئله، راه حل مستقیمی نداشته باشد یا راه رسیدن به جواب آن طولانی و دشوار باشد. شما
می توانید با یک روش منطقی و منظم، پاسخ احتمالی مسئله را حدس بزنید؛ سپس با توجه به شرایط گفته شده در مسئله، حدس خود را بررسی کنید و با توجه به نتیجهء به دست آمده حدس بعدی را بزنید تا کم کم به پاسخ مسئله نزدیک شوید.
تمرین های که در کتاب ریاضی هفتم صفحه 6 برای دانش آموزان آمده است , نسبتا مغلق برای دانش آموزان پایه هفتمی است که در این فیلم آموزشی استاد الهه درویشی این تمرین ها را با توضیح و تشریح کامل حل نموده است.
جزوه ریاضی هفتم فصل 1 راهبردهای حل مسئله (8 صفحه)دانلود
فیلم و جزوه طول سال ریاضی هفتم فصل اول راهبردهای حل مسئله – قسمت دوم
زاویه متمم:
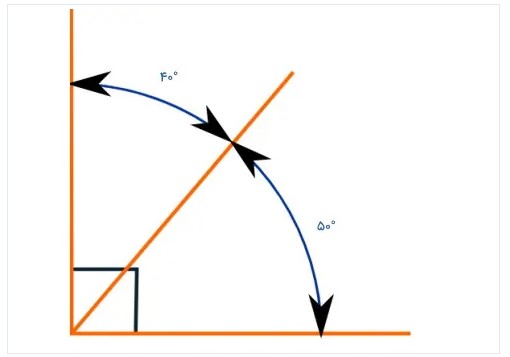
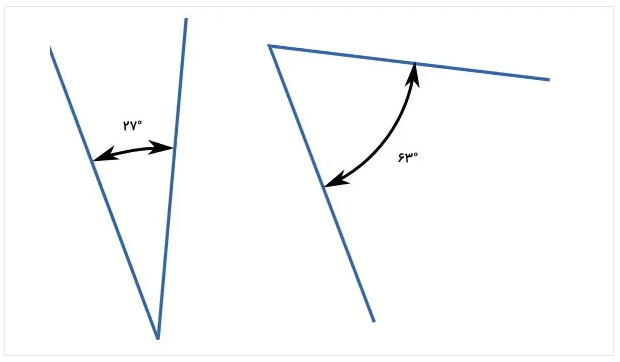
به هر دو زاویه که مجموع آنها برابر با ۹۰ درجه باشد، زاویه متمم میگویند. به عنوان مثال دو زاویه ۴۰ و ۵۰ درجه زاویههایی هستند که با یکدیگر، زاویه راست میسازند. از اینرو، این جفت زاویهها به عنوان زاویههای متمم شناخته میشوند. (شکل الف)
برای متمم بودن زاویه ها, نیازی به مشترک بودن ضلع های آنها نیست. اگر مجموع دو زاویه جدا از هم نیز برابر با 90 درجه باشد آن دو زاویه متمم یکدیگر در نظر گرفته میشوند. (شکل ب)
(الف) از مجموع دو زاویه مجاور ( راس و یک ضلع مشترک) تشکیل شده است.
(ب) از مجموع دو زاویه غیر مجاور که ضلع و راس مشترک با هم ندارند تشکیل شده است.
راهبرد زیرمسئله
مسئلهء پیچیده و چند مرحله ای را به چند مسئلهء ساده تبدیل کنید. از این زیرمسئله ها فهرستی درست کنید؛ سپس به ترتیب به آنها پاسخ دهید. اگر ترتیب زیرمسئله ها را درست تشخیص داده باشید، حل هر زیرمسئله به حل مسئلهء بعدی کمک می کند تا در نهایت به خواستهء اصلی مسئله برسید.
در این فلم آموزشی استاد الهه درویشی به حل مسائل کتاب ریاضی هفتم صفحه 7 میپردازد که موضوع مهم و پرسش برانگیز برای دانش آموزان میباشد.
حل صفحه 7 ریاضی هفتم
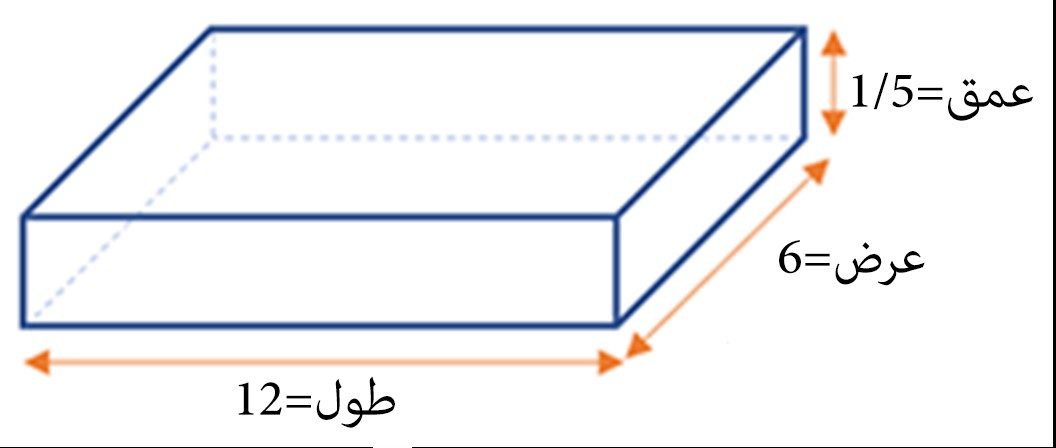
2 – در یک مجتمع مسکونی استخری به طول، عرض و عمق به ترتیب 12, 6 و 1/5 متر وجود دارد. مدیر ساختمان پیشنهاد کرده است که دیوارها و کف استخر ترمیم و بازسازی و سپس رنگ شود. او از یک نقاش خواست تا برآورد کند که انجام این کار چقدر هزینه دارد و به مدیر ساختمان اعلام کند. نقاش ها به طور معمول براساس هر مترمربع برای خودشان دستمزد درنظر می گیرند و قیمت رنگ را هم جداگانه حساب می کنند.
اگر قیمت هر کیلوگرم رنگ ٣٠٠٠٠٠ تومان و دستمزد رنگ کردن هر مترمربع ٢٠٠٠٠ تومان باشد و برای رنگ کردن هرمتر مربع استخر کیلوگرم رنگ مصرف شود، هزینه این کار را حساب کنید.
حل:خوب در نخست یک تصویر برای درک بهتر مسئله ترسیم میکنیم.
الف) مساحت کف استخر را دریابید.
ب ) مساحت دیوار های استخر را دریابید.
ج ) مساحت عمومی استخر را محاسبه کنید.
د ) مقدار رنگ مورد نیاز را دریابید.
ز ) هزینه رنگ مورد نیاز را محاسبه کنید.
ه ) دستمزد نقاش را محاسبه کنید.
ی ) هزینه این کار را محاسبه کنید.
حل:
الف) مساحت کف استخر
ب) مساحت دیوار های استخر را دریابید.
استخر چهار دیوار دارد , چون دیواره های مقابل هم , با هم برابر هستند پس مساحت هر یک از دیواره ها را دریافته و ضرب در 2 میکنیم.
ج ) مساحت عمومی استخر را محاسبه کنید.
د ) مقدار رنگ مورد نیاز را دریابید.
اگر برای رنگ کردن یک متر مربع کیلوگرام رنگ نیاز باشد , پس برای رنگ کردن 126 متر مربع چقدر رنگ نیاز است؟
ز ) هزینه رنگ مورد نیاز را محاسبه کنید.
هزینه یک کیلوگرام رنگ 300000 تومان است , پس هزینه رنگ چند خواهد شد؟
ه ) دستمزد نقاش را محاسبه کنید.
دستمزد رنگ کردن هر متر مربع 20000 تومان است , پس دستمز 126 متر مربع چند خواهد شد؟
ی ) هزینه این کار را محاسبه کنید.
راهبرد حل مسئلۀ ساده تر
برای حل بعضی از مسئله ها،ابتدا مسئله ای ساده تر را که با مسئلهء اصلی در ارتباط است، حل می کنیم. سپس بااستفاده از نتیجه و پاسخ مسئلهء ساده شده، جواب مسئلهء اصلی را به دست می آوریم. برای ساده کردن مسئله می توان از عددهای تقریبی یا عددهای کوچک تر استفاده کرد.
مسئله های که در ریاضی هفتم صفحه 7 و 8 آمده است, مسئله های چالشی برای دانش آموزان پایه هفتمی میباشد. میتوانید حل این مسائل مهم و پیچیده را در فیلم آموزشی ریاضی هفتم فصل اول مشاهده کنید.
اعداد تقریبی
این عددها به دانشآموزان کمک میکنند تا به طور تقریبی مقدار یک عدد دقیق را بدست آورند. به عنوان مثال، اگر دانشآموزان بخواهند مقدار ۴2۶ را به صورت تقریبی بیان کنند، میتوانند از عدد تقریبی ۴0۰ استفاده کنند. زیرا استفاده از عدد تقریبی ۴0۰ نزدیکترین و مناسبترین تقریب به این عدد است.
ریاضی هفتم صفحه 9 در مورد راهبردی است که در این راهبرد معمولا از عبارت های جبری استفاده میشود. عبارت های جبری موضوع مهم و اساسی در ریاضیات میباشد. که از ریاضی پایه هفتم شروع و تا به پایه دوازدهم همیشه با آن سر و کار دارید.
راهبرد روش های نمادین
بسیاری از مسئله ها را می توانیم به کمک نمادهای جبری به یک معادله تبدیل کنیم.از فصل سوم به بعد می توانید از این راهبرد نیز برای حل مسئله استفاده کنید. در بعضی از مسئله ها هم می توانیم از مدل سازی هندسی استفاده کنیم. تبدیل مسئله به یک شکل هندسی و حل هندسی آن نیز نوعی روش نمادین یا مدل سازی به شمار می رود.
در کتاب ریاضی هفتم صفحه 10 مرور بر راهبرد های حل مسئله صورت گرفته است , که یک مرور مفید و کاربردی برای فصل یک کتاب ریاضی کلاس هفتم میباشد. شما میتوانید حل صفحه 10 ریاضی هفتم را در این فیلم آموزشی مشاهده نموده و از فیلم های آموزشی بنیاد آموزش ملی استفاده مثمر نمایید.